Geometria triunghiului

[Admin]

In exteriorul triunghiului oarecare $\Delta ABC$ se construiesc 3 triunghiuri echilaterale.
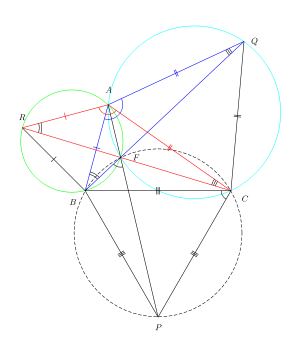
Să se arate că centrele acestora formează un triunghi echilateral.

Asta e o problemă foarte cunoscută ..
Indicațiile date de George Polya în cartea lui celebră "Descoperirea în Matematică" (pag. 210) merge către rezolvarea trigonometrică (G.P. nu dă o rezolvare).
Am dat o soluție rapidă trigonometrică, simplă dar cu multe calcule (mai bine de 1 pagină) - folosindu-mă de teorema cosinusului și teorema sinusurilor (și apoi de multe calcule) ...

Știam de o problemă legată de asta: anume să se arate că AA₁ = BB₁ = CC₁ (vezi și cartea de Transformări geometrice, de Smaranda/Soare - o carte foarte bună de transformări geometrice ... Pb. 21, pag 66)

Se observă că la o rotație de 60^o (în sensul acelor de ceasornic) a triunghiului ACA₁, în jurul lui C, se obține triunghiul B₁CB ... Deci AA₁ = BB₁ .. și prin analogie vor fi egale și cu CC₁ (sau altfel spus triunghiurile ACA₁ și B₁CB sunt congruente, și rezultă de aici tripla egalitate de segmente ... Eu o să folosesc demonstrația cu rotația, pentru că folosesc și la altceva ...)

Notez cu G, G₁, G₂ şi G₃ centrele de greutate ale triunghiurilor din figură.

Medianele se taie la 2 treimi de vârf și o treime de latură, deci cu Thales și apoi asemănarea triunghiurilor avem că GG₁ || AA₁ şi în plus GG₁ = 1/3 AA₁. Cum AA₁ = BB₁ = CC₁ rezulta cu GG₁ = GG₂ = GG₃.

Deci G este chiar centrul cercului circumscris triunghiului G₁G₂G₃ (și mai trebuie doar să arăt doar că în jurul lui G sunt 3 unghiuri de 120^o - unghiurile formate de segmentele trasate cu roșu ...)

Cum segmentele AA₁, BB₁, CC₁ se obțin unul din altul prin rotații de 60^o (deci formează un unghi ascuțit de 60^o și unul obtuz de 120^o) înseamnă că același lucru e valabil și cu GG₁, GG₂ și GG₃ (care sunt paralele cu AA₁, BB₁ și CC₁).

Uitându-ne în triunghiul G₁G₂G₃ nu puteam avea de exemplu ca unghiul G₁GG₂ să aibă 60^o, fiindcă ar însemna că celelalte 2 unghiuri adică G₂GG₃ și G₃GG₁ să facă împreună restul de 300^o, ori ele au fie 60^o fie 120^o .. deci imposibil ... Deci obligatoriu toate aceste 3 unghiuri au 120^o , deci triunghiul G₁G₂G₃ e echilateral ...

[Admin]

Căutam niște generalizări și am găsit altele (plus că am văzut că Teorema poartă numele lui Napoleon .. nu mai ştiu dacă am mai citit de asta vreodată, chiar dacă problema e foarte cunoscută ... Totuși e precizat pe un site
".. Remarks: The attribution to Napoléon Bonaparte (1769-1821) is traditional, but dubious.. ")

Generalizarea (într-o anumită direcție) => Teorema Napoleon-Barlotti (1955, redescoperita de L. Gerber în 1980)

Ideea se pare că a venit de la teorema lui V. Thébault's (1937) .. unde se vedea că merge pt cazul n=4 ... nu numai 3, ca în cazul th. Napoleon ... Dar totuși trebuie spus ce înseamnă poligon regulat-afin (merge la triunghiuri oarecare - cazul n=3 - sau paralelograme - cazul n=4)

(Deci avem un paralelogram .. pe laturile lui se construiesc în exterior (merg discuțiile și în interior !) niște pătrate.
Centrele acestora formează un pătrat ...)

Teorema Napoleon-Barlotti (adică generalizarea)
Pe laturile unui poligon regulat-afin cu n laturi se construiesc n poligoane regulate (cu n laturi fiecare).
Centrele acestor poligoane regulate formează un poligon regulat (cu n laturi).

---

Ceea ce căutam eu e altceva (și are legătură cu teorema lui Vecten .. deci cazul 4 ... vroiam să ştiu dacă e deja demonstrată generalizarea .. o anume generalizare .. dar nu am găsit deocamdată .. și văd că pt cazul n nu prea e ușor de demonstrat ..)

E așa :
Pe laturile unui triunghi oarecare se construiesc în exterior poligoane regulate de gradul n. Dacă unim fiecare vârf al triunghiului cu centrul poligonului regulat construit folosind latura opusă, se obțin 3 drepte concurente ?

Cazul n=4 este Teorema lui Vecten (care se demonstrează mai scurt cu arii .. asemănare ..etc)

---

PS 1



Pentru cazul n=3 poate poate folosi punctul lui Torricelli (sau punctul lui Fermat).
(în cartea Smaranda/Soare, pag. 66, ex 21, "Transformări geometrice" se spune greșit că acel punct de intersecție ar fi la jumatea lor ! - dacă ar fi fost aș fi avut deja demonstrația ...)


PS 2 Teorema e cunoscută ! (chiar e generalizare și pentru cazul n ...)
Si văd că e din 1999 ! (generalizarea th. lui Fermat-Torricelli ...)

Demonstrația e destul de lungă ...
Am găsit aici una trigonometrică A-generalization-of-the-Fermat-Torricelli-point ...

*** Această postare conţinea multe imagini.
Din păcate site-ul ImageShack (unde erau găzduite) a şters multe din ele.. nu cunosc motivul

[Admin]

$\Delta ABC$ este un triunghi oarecare iar $K$ este un punct oarecare situat în interiorul triunghiului.
Punctele de intersecţie se construiesc ca in imaginea de mai jos.

Atunci avem egalitatea :

$\displaystyle \dfrac{1}{\dfrac{AD}{DX}+\dfrac{1}{2}}+\dfrac{1}{\dfrac{BE}{EY}+\dfrac{1}{2}}+\dfrac{1}{\dfrac{CF}{FZ}+\dfrac{1}{2}}=\dfrac{2}{3}$

Demonstraţia nu este tocmai uşoară.
Una din ele se regăseşte la adresa : cut-the-knot.org