Problemă (
Problemă clasică şi foarte importantă - Cu una din demonstraţiile cele mai "naturale")
Dacă
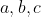
sunt numere raţionale şi
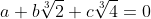
atunci

.
Problema este valabilă dacă înlocuim pe
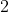
cu orice număr prim
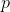
.
Deci dacă
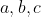
sunt raţionale iar

atunci

.
Rezolvare :
Observaţia 1 : Daca macar unul din numerele
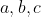
este nul atunci evident ca si celelalte
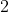
sunt nule, fiindca
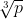
si
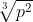
sunt numere irationale (am facut aceasta observatie pentru o demonstratie cat mai completa si mai riguroasa).
Observaţia 2 : Presupunand deci numerele
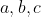 nenule
nenule atunci, scriindu-le ca fractii ordinare, aducand apoi la acelasi numitor, inmultind relatia cu respectivul numitor comun obtinem
noi numere 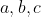
(care satisfac relatia din ipoteza) dar care sunt
intregi .. si simplificand relatia cu
)
putem considera numerele
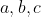
chiar numere
intregi si
prime intre ele (Deci
=1)
).
Reformulăm atunci problema :
Dacă avem
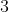
numere
întregi nenule 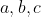 prime între ele
prime între ele iar
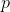 prim
prim atunci nu putem avea :

.
Demonstratie. Facem apel la
metoda reducerii la absurd.
Presupunem prin absurd ca avem
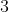
numere
intregi nenule 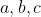 prime intre ele
prime intre ele iar
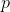 prim
prim astfel incat :

.
(***)Demonstratia propriu zisa (
prin aceasta abordare) face apel la formula din prima postare in topic. Folosim deci :
(x^2 + y^2 + z^2 - xy - xz - yz))
pentru

.
Evident
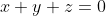
, din ipoteza, si atunci

adica :

si de aici
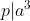
dar
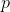
fiind prim trebuie sa avem
 (1)
(1)Scriem
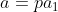
, inlocuim, simplificam relatia prin
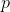
si obtinem :
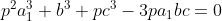
si analog obtinem
 (2)
(2)Scriem

, inlocuim, simplificam relatia prin
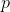
si obtinem :

si analog obtinem
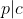 (3)
(3)Relatiile
(1) +
(2) +
(3) inseamna ca
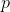
divide toate cele
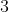
numere
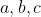
deci acestea nu ar mai fi prime intre ele ..
Contradictie cu presupunerea facuta initial la
(***), iar demonstratia este completa.
QED